2025. 2. 16. 20:02ㆍ카테고리 없음
유튜브 알고리즘이 추천해 주는 영상을 보다가 다음과 같은 영상을 보게 되었다. 영상 길이도 짧고 내용도 잘 정리되어서 간단하니 영상을 먼저 봐주길 바란다.
영상

위 문제는 고난도 수학 문제집인 블랙라벨 문제집의 레벨 3 난이도 항등식 문제다. 이 글에서는 위의 항등식 문제에 대한 특이한 풀이와, 풀이의 증명을 알아볼 것이다. 고등학교 수준에서 정석인 풀이는 다음과 같다.
- f가 다항식인 걸 확인하면, f(x^2)과 x^2f(x)의 차수가 같다 -> f(x)는 2차식 유도 가능. 거기에 f(0) = 8로, f(x) = ax^2 + bx + 8
- 숫자 몇 개 계산 편한 거 넣어보면서 a, b 찾기 (노가다 계산 필요)
1까지는 수학 좀 한다면 누구나 다 하지만, 2에서는 계산이 문제다. 계산을 많이 요구하는 풀이보단 계산을 적게 요구하는 풀이가 항상 더 좋기 마련이다. 그럼, 계산을 줄이는 풀이를 알아보자. 바로 멱영원(Nilpotent)을 사용하는 풀이인데, 멱영원이란 0이 아닌 수 중에 N제곱하면 0이 되는 수를 말한다(ε^n = 0, ε != 0). 기호로는 ε이라고 자주 표기하며 '입실론(Epsilon)'이라고 읽는다. 이번 글에서 사용할 멱영원은 n이 2인 경우로, (ε^2=0, ε != 0) 인 수 ε이다.
여기서 의문이 드는 게, 그런 수가 존재할 수 있냐는 것이다. 수 자체가 실수에도 복소수에도 없는 수여서 우리의 수에 대한 직관들이 작동하지 않아, 예측하지 못한 성질이 꽤 많을 것이다. 예를 들어 1/ε은 뭘까? 실수에 ε을 추가한 수 체계에서 ε의 역원인 1/ε이 존재한다고 가정해 보자. 그러면 (1/ε)^2 = 1/0이라는 결과를 얻기에, 저런 수는 존재해선 안 된다. 즉, ε을 포함하는 실수는 곱셈역원(1/x)조차 정의되지 않는 역대급 쓰레기(...) 수 체계라는 것이다. 딱 보니 지수, 로그, 삼각함수 같은 함수들 역시 이 ε을 포함한 실수에서는 잘 작동하지 않을 것이다. 이런 수 체계에서 다항식의 항등식이 잘 작동한다는 것이 얼마나 비직관적인 일인지 느껴지는가?
그럼 이제 이게 왜 되는지 살펴보자. 질문을 구체화하면, "실수에서 정의된 다항식의 항등식은, ε을 포함하는 실수에서도 성립한다."이다. 실수에서 정의된 다항식에 대해서 항등식이 성립한다는 것은, 임의의 다항식 P(x)에 대하여 x에 어떤 실수를 대입해도 0이 나온다는 것과 동치이다. 항등식에서 우변을 좌변으로 전부 넘기고, 그 상태의 좌변을 P(x)로 보면 된다:
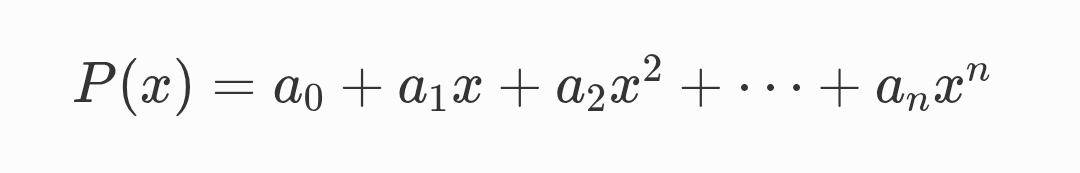

여기서 알아야 할 것이, 이건 근을 찾는 방정식이 아니라 항등식이다. 위의 식이 모든 실수 x에 대해서 성립하려면, x^0, ..., x^n 각각을 전부 0으로 만들어야 하기 때문에, a_0, ..., a_n이 전부 0이어야 한다. 그런데 ε을 포함하는 실수들이 전부 a + bε꼴로 표현되는 걸 생각해보면, (a + bε) × 0 = 0이라, x에 어떤 a + bε을 대입하든 똑같이 0이 나올 것이다. 즉, 우리는 방금 모든 ε을 포함하는 실수에 대해서 항등식이 성립하는 걸 보였다. 증명 끝!
이긴 한데 조금 아쉽다.. 위의 논리는 꼭 멱영원 ε이 아니라 어떤 이상한 수를 가져와도 성립할 것이다. 그야 증명에서 멱영원의 성질인 (ε^2=0, ε!=0)을 전혀 쓰지 않았다. 사용한 성질이라고는 모든 실수에 대해 다항식이 0과 동일하려면 각 항의 계수가 전부 0이어야 한다는 것이다. 그렇다면 실수에 아주 이상한 숫자를 하나 추가하면, 이걸 만족하지 못하게 만들 수도 있을까? 그런 수가 갖는 조건은 무엇일까?
사실, 그런 수는 존재하지 않는다! 대수학의 기본정리에 의해서 실수계수 n차 다항식은 복소수 범위에서 중복을 허용하여 근을 n개만 가질 수 있고, 따라서 어떤 P(x)를 들고와도 c(x-a1)...(x-an) 꼴로 인수분해가 된다. 근데 저 식에 아무 실수나 대입해도 0이 나와야 하니 c = 0이 되는 수밖에, 즉 P(x) = 0이 되는 수밖엔 없다. 우리는 현재 실수의 성질만 사용했다. 실수에 수를 하나 추가하는 확장에서 위의 논의를 무력화시키려면, c = 0이어도 P(x)가 0이 안되게 만들면 된다. 즉, 그런 수를 t라고 한다면, t × 0 != 0이면 된다. 그런데... 사실 다항식이라는 건 '환(Ring)'이라고 하는 대수 구조로 정의되는 건데, 문제는 저렇게 0과 곱해서 0이 안되는 수는, 환의 정의 상 존재하면 안된다는 것이다. 그래서 결국 실수에 숫자를 하나 추가해서 다항식을 성립시키지 않는 수는 없는 것이다.
결론이 조금 찝찝할 수도 있다. 환(Ring)이 뭔가? 대수 구조는 뭔가? 다항식이 왜 저거랑 연관이 있는가?... 위의 내용들은 다음 글에서 자세히 다뤄보도록 하고, 이번 글은 여기서 마치겠다. 추가로 더 읽어보면 좋은 자료들을 올린다.
이원수(ε)
대수학의 기본 정리
환(Ring)